Qu'est-ce qu'un algorithme : définition, types et exemples

Diagrammes

> Connaissances en diagrammes de base > Qu'est-ce qu'un algorithme : définition, types et exemples

Un algorithme est une démonstration étape par étape du traitement des données ou de la résolution de problèmes. Cette page présentera la définition, les types et les applications de l'algorithme.

Un algorithme peut être décrit comme une procédure ou une formule pour la résolution de problèmes. Les algorithmes peuvent être largement utilisés dans divers domaines, la programmation informatique, les mathématiques et les vies quotidiennes. Ensuite, quelle est la définition algorithme ? Combien y a-t-il de types et de quelle manière peuvent-ils être appliqués ?

Définition algorithme

L'algorithme peut être défini comme "Une séquence d'étapes à effectuer pour une sortie requise d'une certaine entrée donnée". Il existe 3 caractéristiques principales de l'algorithme de sa définition :

L'objectif essentiel d'un algorithme est d'obtenir une sortie spécifique ;
Un algorithme comporte plusieurs étapes continues ;
La sortie vient après que l'algorithme a terminé l'ensemble du processus.

Donc, fondamentalement, tous les algorithmes fonctionnent logiquement tout en suivant les étapes pour obtenir une sortie pour une entrée donnée.

Types d'algorithme

Les algorithmes peuvent être classés en 3 types en fonction de leurs structures :

Séquence : Ce type d'algorithme se caractérise par une série d'étapes, et chaque étape sera exécutée l'une après l'autre.
Branchement : Ce type d'algorithme est représenté par les problèmes « si ». Si une condition est vraie, la sortie sera A, si la condition est fausse, la sortie sera B. Ce type d'algorithme est également appelé « type de sélection ».
Boucle : Pour ce type, le processus peut être exécuté à plusieurs reprises sous une certaine condition. Il est représenté par des problèmes « oui » et « non ». Mais assurez-vous que le processus se terminera après un certain nombre de boucles sous la condition. Ce type d'algorithme est aussi appelé « type de répétition ».

Exemples d'algorithme simples

Comme mentionné précédemment, les algorithmes peuvent être utilisés dans de nombreux domaines, et ils sont souvent représentés sous forme de diagramme pour la compréhension visuelle. En d'autres termes, un logigramme est un diagramme qui représente un algorithme, montrant les étapes dans diverses boîtes et affiche le processus en connectant les cases ensemble. Voici quelques exemples d'application d'algorithme dans les formes de logigramme.

Voici des exemples d'algorithme simple dans le logigramme.

Télécharger gratuitement l'outil pour la création de logigramme

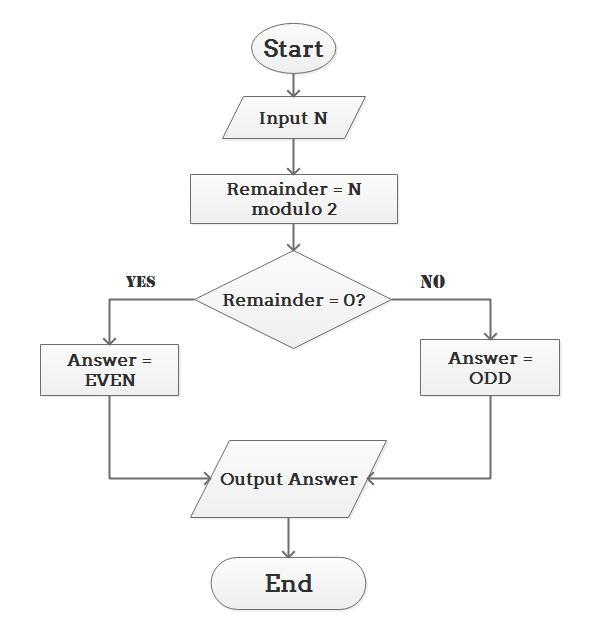
1. Exemple d'algorithme - logigramme en mathématique

Déterminer et exporter si le nombre N est pair ou impair

exemple d'algorithme en mathématique

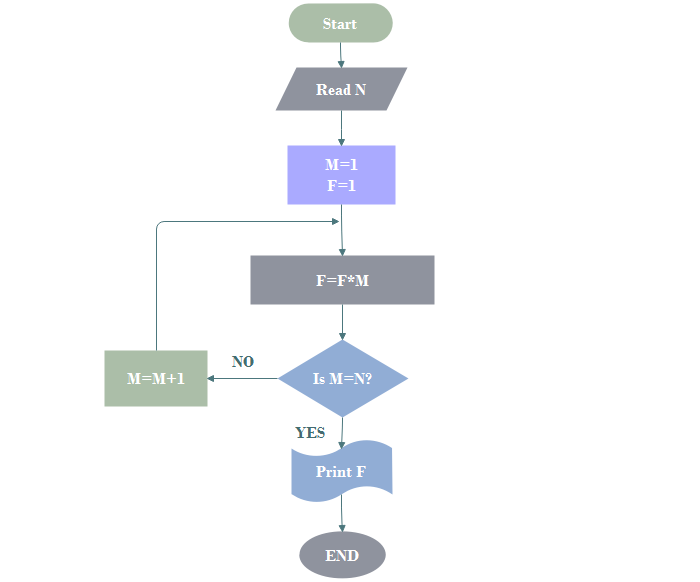
2. Exemple d'algorithme dans le logigramme pour la programmation informatique

Dessinez un logigramme pour calculer le factoriel N (N!)

exemple d'algorithme pour la programmation informatique

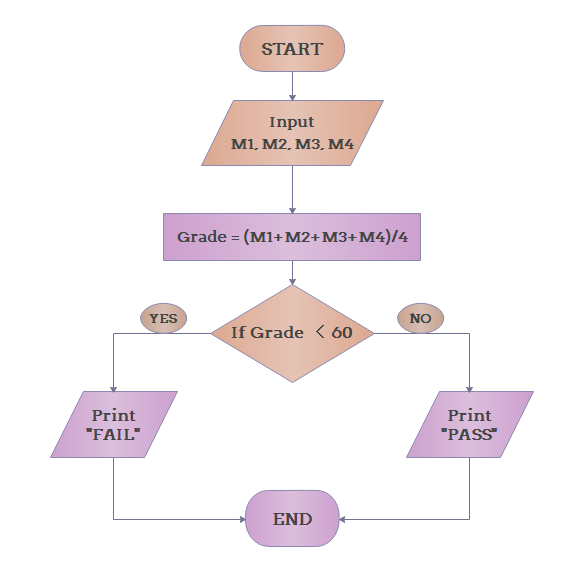
3. Exemple d'algorithme - logigramme pour la vie quotidienne

Déterminez si l'élève a passé l'examen ou non

exemple d'algorithme pour la vie quotidienne

Les exemples ci-dessus donnent une démonstration claire des applications d'algorithmes en mathématiques, programmation informatique et vie quotidienne. La création d'un logigramme pourrait être la meilleure façon de représenter un algorithme. Plus d'exemples se référer aux liens suivants :

Expliquer l'algorithme et le logigramme avec des exemples

Exemples de logigramme

Télécharger Version Windows Version Mac Version Linux

Qu'est-ce qu'un algorithme : définition, types et exemples

Diagrammes

Définition algorithme

Types d'algorithme

Exemples d'algorithme simples

Commencez! Vous allez adorer ce logiciel de diagramme facile à utiliser.