데이터 시각화의 두 기둥, 히스토그램 vs. 막대그래프
데이터 시각화의 두 기둥, 히스토그램 vs. 막대그래프
본문을 통해 히스토그램과 막대그래프의 차이에 대해 알아보세요. 이드로우맥스(EdrawMax)는 AI 기능을 탑재하고 있어 다이어그램을 더욱 간편하게 작성 할 수 있습니다. 지금 바로 EdrawMax AI 기능을 이용하여 다이어그램을 만들어 보세요!
데이터를 시각적으로 표현하는 방법은 다양합니다. 그 중에서 히스토그램과 막대그래프는 많은 사람들이 자주 사용하는 도구입니다. 하지만 이 두 가지 그래프는 비슷해 보이지만, 그 용도와 표현하는 데이터의 유형에서 중요한 차이가 있습니다.
히스토그램은 연속형 데이터의 분포를 나타내는 데 최적화되어 있으며, 데이터가 특정 구간에 어떻게 분포되어 있는지를 시각적으로 보여줍니다. 반면, 막대그래프는 범주형 데이터를 비교하는 데 사용되며, 각 범주가 가진 크기나 수치를 쉽게 비교할 수 있도록 도와줍니다.
이번 글에서는 히스토그램과 막대그래프의 정의, 주요 차이점, 그리고 각각의 활용 사례에 대해 자세히 살펴보겠습니다. 이러한 차이를 이해하는 것은 데이터 분석이나 프레젠테이션에서 올바른 시각화 도구를 선택하는 데 도움이 될 것입니다. 데이터의 형태에 따라 적절한 그래프를 선택함으로써, 정보를 더욱 효과적으로 전달할 수 있습니다.
Part 1: 히스토그램이란? 유형, 구성 요소와 예시
1) 히스토그램이란?
히스토그램은 데이터의 분포를 시각적으로 표현하는 막대 그래프의 한 유형으로, 연속적인 데이터 분포를 간편하게 파악하는 데 유용합니다. 히스토그램은 각 데이터 구간(범위)에 속하는 데이터의 빈도수를 막대 높이로 나타내어, 데이터가 특정 구간에 얼마나 집중되어 있는지, 분포가 대칭적인지, 특정 패턴이 있는지 등을 한눈에 보여줍니다.
2) 히스토그램의 유형
히스토그램은 데이터 분포의 형태에 따라 다양한 유형으로 구분할 수 있습니다.
• 정규 분포형 히스토그램 (Normal Distribution Histogram): 가운데 부분이 높고 양쪽으로 대칭되는 종 모양의 분포를 보입니다. 주로 자연적 현상에서 많이 나타나는 패턴입니다.
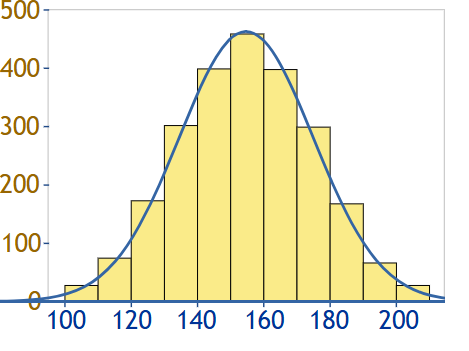
출처: https://www.mathsisfun.com/data/images/normal-distribution.svg
• 치우침 분포형 히스토그램 (Skewed Distribution Histogram): 데이터가 한쪽으로 치우쳐 있는 경우, 좌측 또는 우측으로 긴 꼬리를 가진 비대칭형입니다. 예를 들어, 소득 분포에서 저소득자가 많은 경우 좌측으로 치우친 분포가 나타납니다.
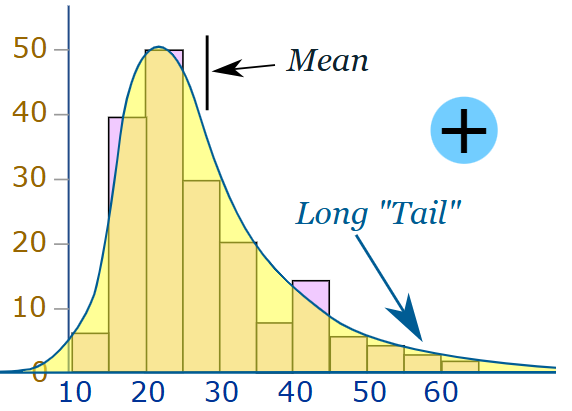
출처: https://www.mathsisfun.com/data/images/skewed-distribution.svg
• 이중봉형 히스토그램 (Bimodal Histogram): 두 개의 봉우리를 가진 분포로, 두 개의 뚜렷한 그룹이 있는 데이터에서 발생할 수 있습니다.
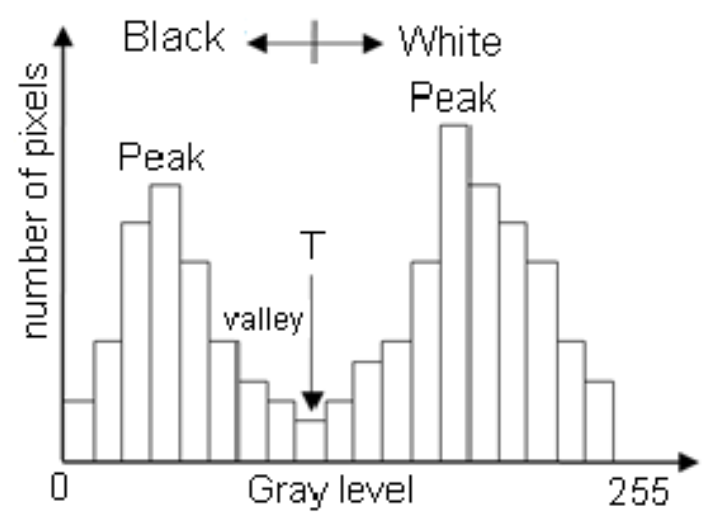
출처: https://www.researchgate.net/figure/Histogram-of-a-sample-gray-level-bimodal-image-T-is-the-threshold-value_fig1_233814424
• 균등 분포형 히스토그램 (Uniform Distribution Histogram): 각 구간에 속하는 데이터의 빈도수가 거의 일정할 때 나타나는 분포입니다.
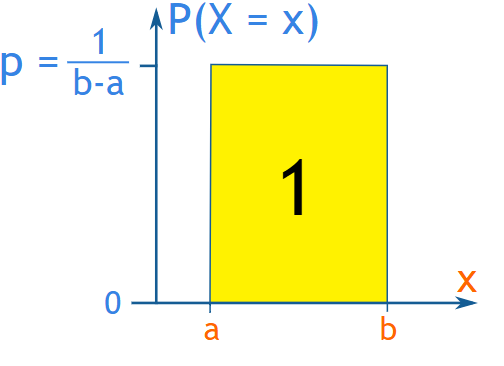
출처: https://www.mathsisfun.com/data/images/uniform-distribution.svg
3) 히스토그램의 구성요소
• 구간(bins): 데이터가 분할된 범위를 의미합니다. 구간의 크기와 개수는 히스토그램의 해상도와 해석에 중요한 영향을 줍니다.
• 빈도(frequency): 각 구간에 속하는 데이터의 개수를 의미하며, 막대의 높이로 표현됩니다.
• x축: 데이터의 값 범위를 나타내며, 구간을 기준으로 데이터 분포를 나눕니다.
• y축: 각 구간에 해당하는 데이터의 빈도를 나타냅니다.
4) 히스토그램의 예시
학생들의 수학 점수 데이터를 히스토그램으로 나타낼 수 있습니다. 여기에서 x축은 점수 범위(구간)이고, y축은 그 점수 구간에 속하는 학생 수(빈도)를 나타냅니다. 이 히스토그램을 보면 점수 분포가 어느 범위에 집중되어 있는지, 평균이 어디에 가까운지 쉽게 파악할 수 있습니다.
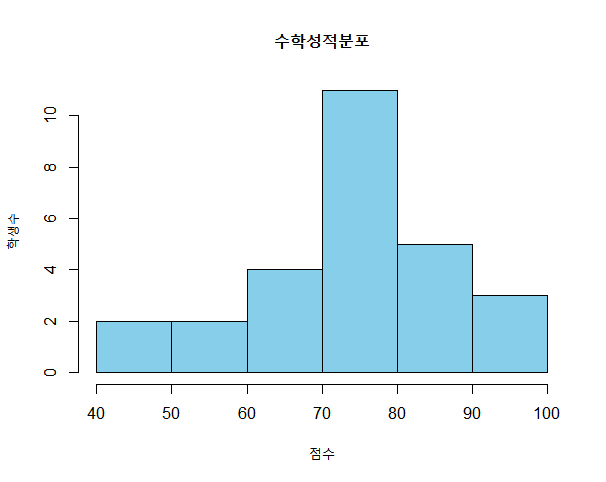
출처: https://thinking-atelier.tistory.com/22
히스토그램은 데이터 분석에서 빈도 분포를 시각적으로 표현하는 기본 도구로, 데이터를 더 깊이 이해하는 데 중요한 역할을 합니다.
Part 2: 막대그래프란? 막대 그래프의 종류와 예시
1) 막대그래프란?
막대 그래프는 데이터의 수치를 막대의 길이 또는 높이로 표현하여 데이터를 비교하고 분석하는 데 사용되는 시각적 도구입니다. 각 막대는 특정 범위나 항목을 나타내며, 막대의 길이(또는 높이)는 해당 값의 크기를 나타냅니다. 막대 그래프는 데이터를 한눈에 비교하기 쉬워서, 다양한 분야에서 널리 사용됩니다.
2) 막대 그래프의 종류와 예시
• 수직 막대그래프 (Vertical Bar Graph): 막대가 수직으로 세워져 있는 형태입니다. 일반적으로 카테고리별로 값을 비교할 때 많이 사용됩니다.
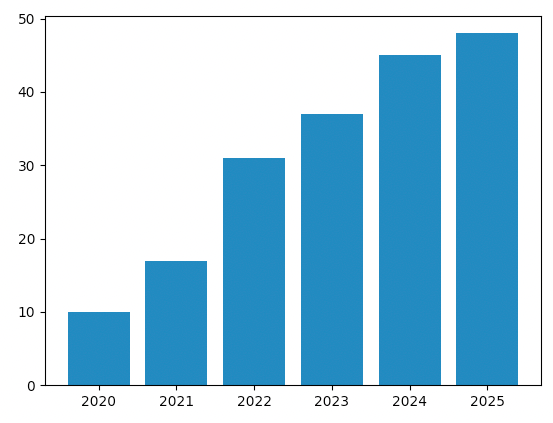
출처: https://cosmosproject.tistory.com/427
• 수평 막대그래프 (Horizontal Bar Graph): 막대가 수평으로 배치된 형태입니다. 카테고리가 길거나 많은 경우에 가독성이 좋습니다.
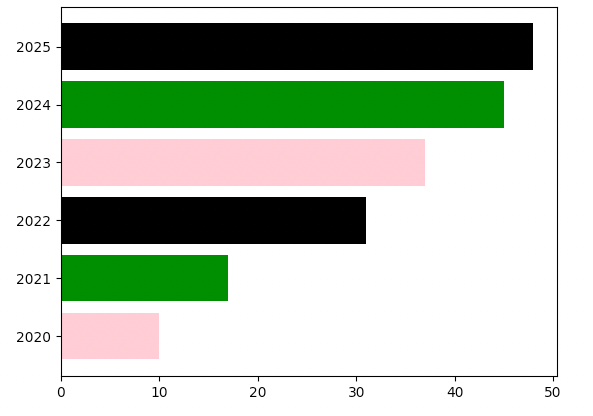
출처: https://cosmosproject.tistory.com/427
• 누적 막대그래프 (Stacked Bar Graph): 각 막대가 여러 부분으로 나누어져 각 부분의 합으로 전체 값을 나타냅니다. 각 부분은 서로 다른 카테고리를 나타냅니다.
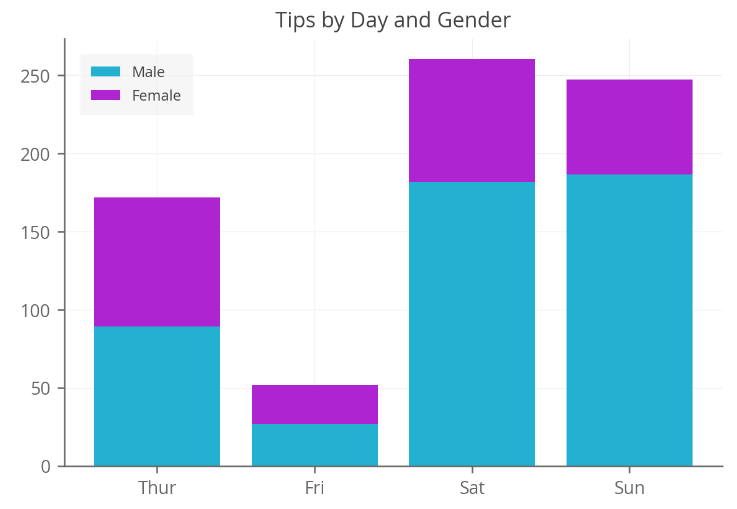
출처: https://www.pythoncharts.com/matplotlib/stacked-bar-charts-labels/
• 군집 막대그래프 (Grouped Bar Graph): 여러 카테고리를 그룹으로 묶어 각 그룹의 값을 비교할 수 있도록 한 형태입니다. 각 그룹 내에서 여러 개의 막대가 존재합니다.
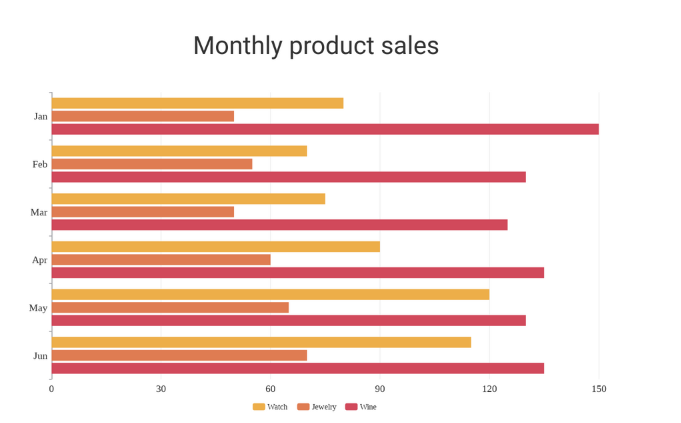 출처:https://online.visual-paradigm.com/ko/charts/templates/grouped-bar-charts/grouped-bar-chart/
출처:https://online.visual-paradigm.com/ko/charts/templates/grouped-bar-charts/grouped-bar-chart/
Part 3: 히스토그램과 막대그래프의 차이
1. 데이터의 종류
• 히스토그램: 연속적인 데이터를 다룹니다. 특정 구간에 속하는 데이터의 빈도를 보여주기 위해 사용되며, 연속적 숫자 데이터(예: 온도, 시간, 거리)를 구간별로 나누어 표현합니다.
• 막대그래프: 범주형 데이터를 다룹니다. 서로 다른 범주(예: 나라별 인구, 제품별 판매량)를 비교하는 데 사용되며, 막대가 특정 항목이나 범주를 나타냅니다.
2. 막대 간 간격
• 히스토그램: 막대들 사이에 간격이 없으며 붙어있습니다. 이는 히스토그램이 연속적인 데이터 구간을 나타내기 때문입니다.
• 막대그래프: 막대들 사이에 간격이 있습니다. 범주형 데이터를 나타내기 때문에 각 항목이 독립적입니다.
3. x축 값의 의미
• 히스토그램: x축은 ‘연속적인 데이터 범위(구간)’를 나타냅니다. 예를 들어, 10-20, 20-30과 같이 구간으로 나뉩니다.
• 막대그래프: x축은 개별적인 범주나 항목을 나타냅니다. 예를 들어, 국가 이름, 제품 유형, 학과명 등이 될 수 있습니다.
4. 목적
• 히스토그램: 데이터의 분포와 밀도를 파악하는 데 주로 사용됩니다. 예를 들어, 시험 점수의 분포를 보면 특정 점수대에 몇 명이 속하는지 알 수 있습니다.
• 막대그래프: 범주 간 데이터의 비교에 주로 사용됩니다. 예를 들어, 다양한 제품의 판매량을 비교할 때 각 제품에 대한 데이터를 별개의 막대로 나타냅니다.
<히스토그램 vs 막대그래프 비교>
|
요소 |
히스토그램 |
막대그래프 |
|
데이터 유형 |
연속형 데이터 |
비연속적 (범주형) 데이터 |
|
막대 간 간격 |
막대 사이 간격 없음 |
막대 사이에 간격 있음 |
|
X축 |
구간을 표현 |
개별 범주를 표현 |
|
목적 |
데이터의 분포를 시각적으로 나타내기 위해 사용 |
범주 간 비교를 위해 사용 |
Part 4: EdrawMax로 히스토그램과 막대그래프 제작하기
1) 히스토그램 만들기
① EdrawMax 실행: 프로그램을 실행하고 ‘새로 그리기’를 시작합니다.
이드로우맥스
올인원 다이어그램 소프트웨어
- 강력한 호환성: Visio,MS office 등 파일 호환 가능
- 다양한 운영체제: (윈도우,맥,리눅스,ios,android)
② 차트 템플릿 선택: 상단 메뉴에서 삽입을 클릭하고 ‘차트’ 카테고리를 선택한 후, 원하는 형식의 템플릿을 찾아 선택합니다.
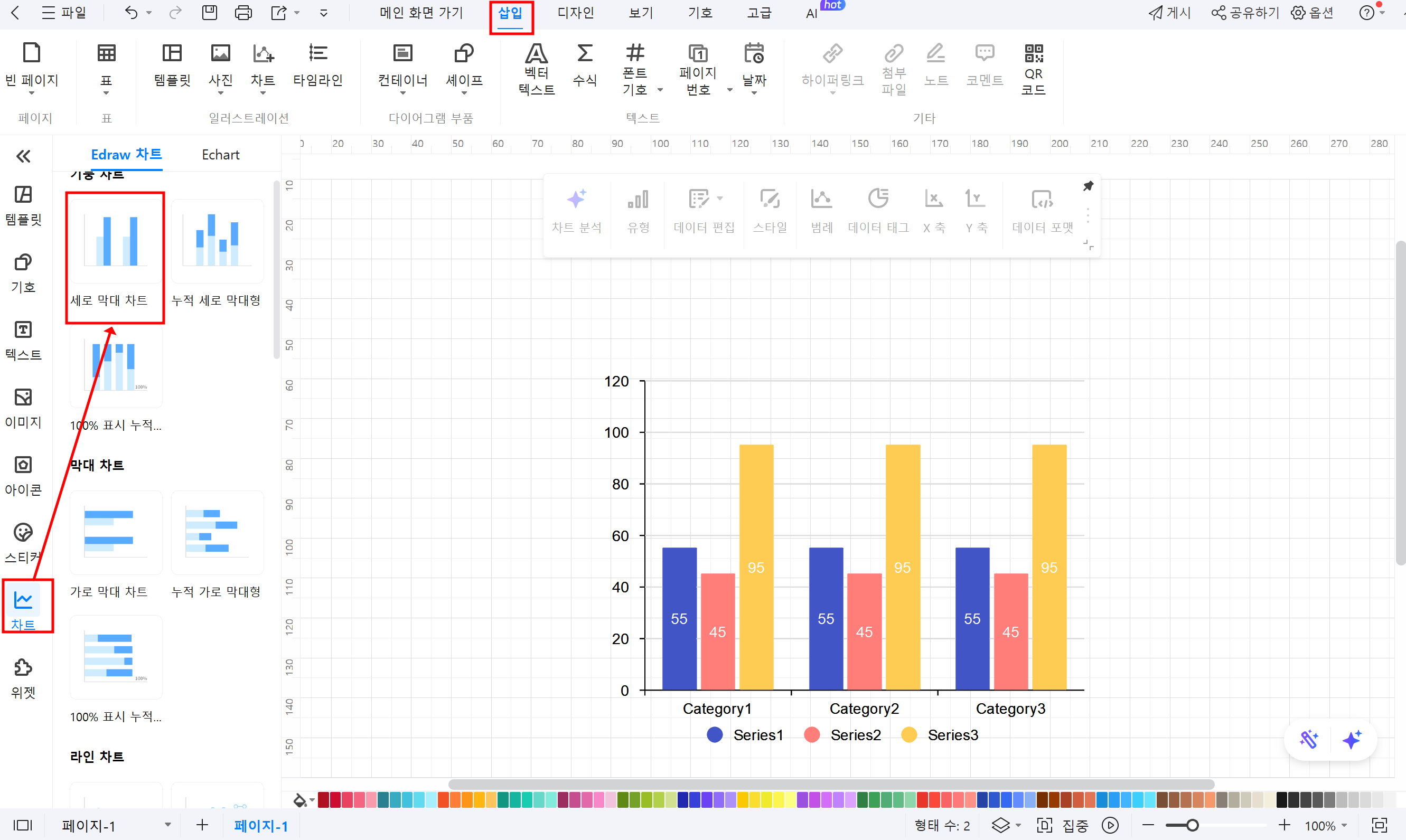
③ 데이터 입력: 플로팅 패널의 데이터 편집을 클릭하여 우측 엑셀형식의 표에서 히스토그램의 각 구간에 해당하는 데이터를 입력합니다.
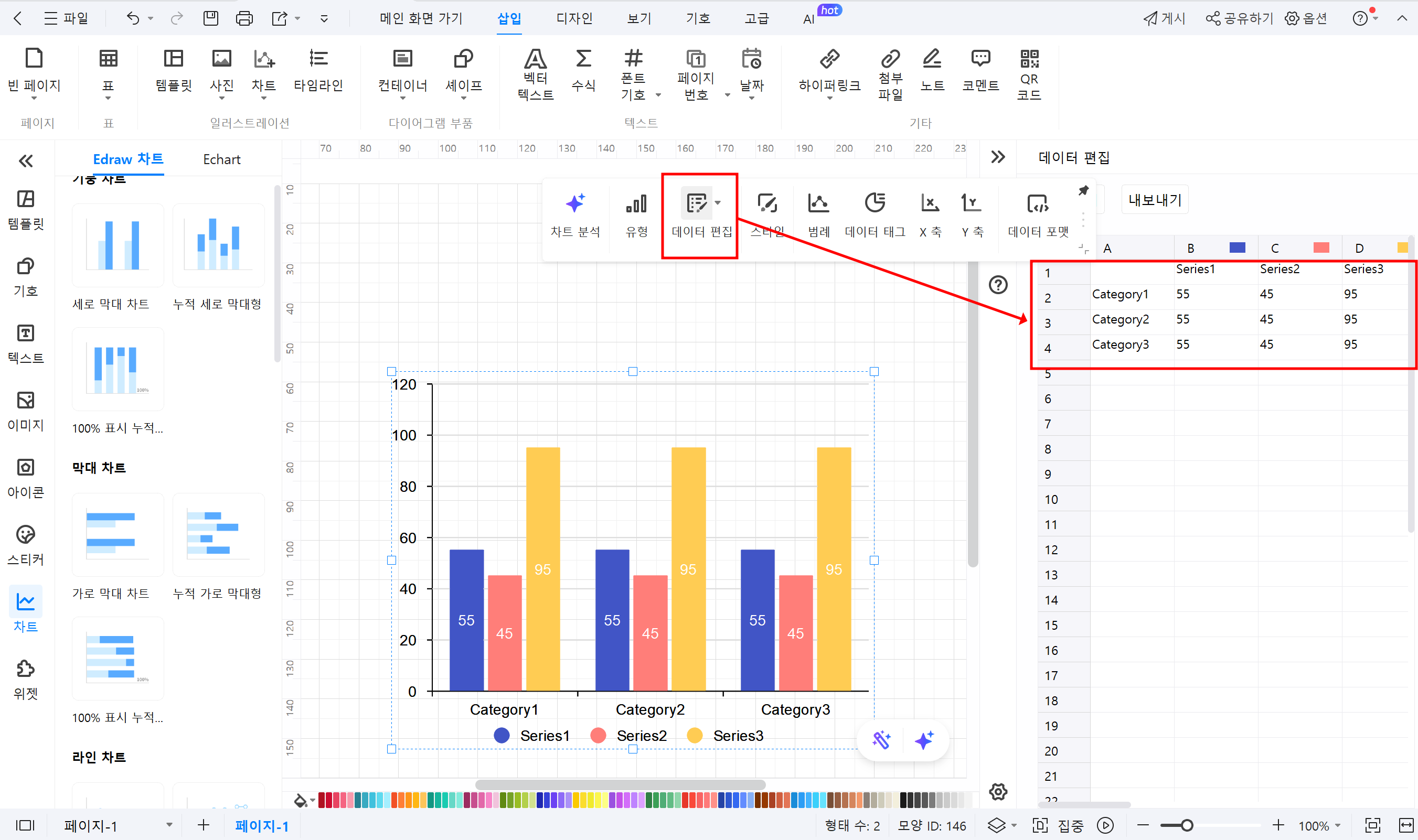
막대 간격 설정: ‘스타일’ -> ‘간격’ 을 ‘0’으로 수정하여 히스토그램 형식에 맞게 조절합니다.
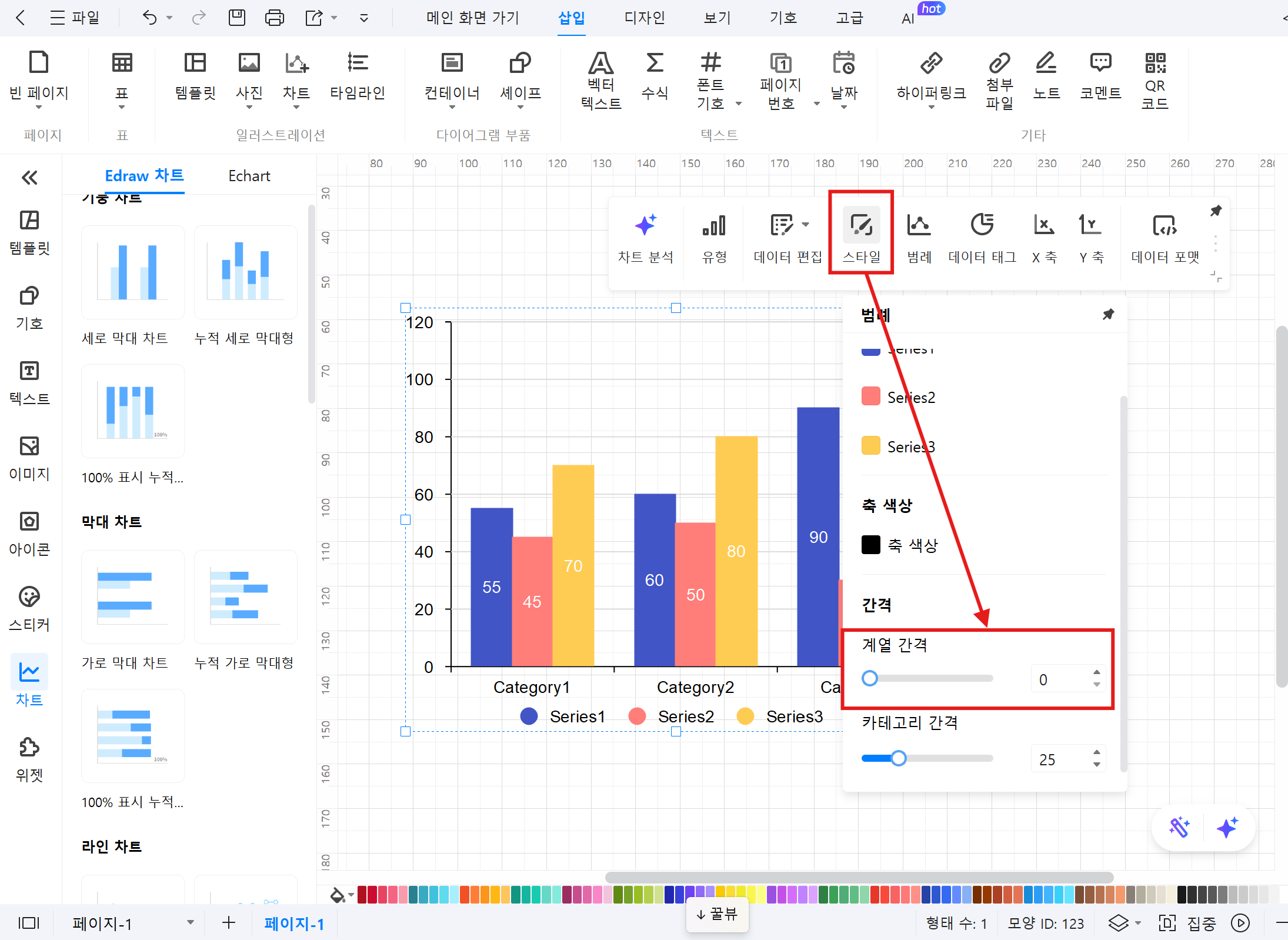
④ 스타일 수정: 그래프 색상, 막대 너비, 레이블 등을 입맛에 맞게 수정합니다.
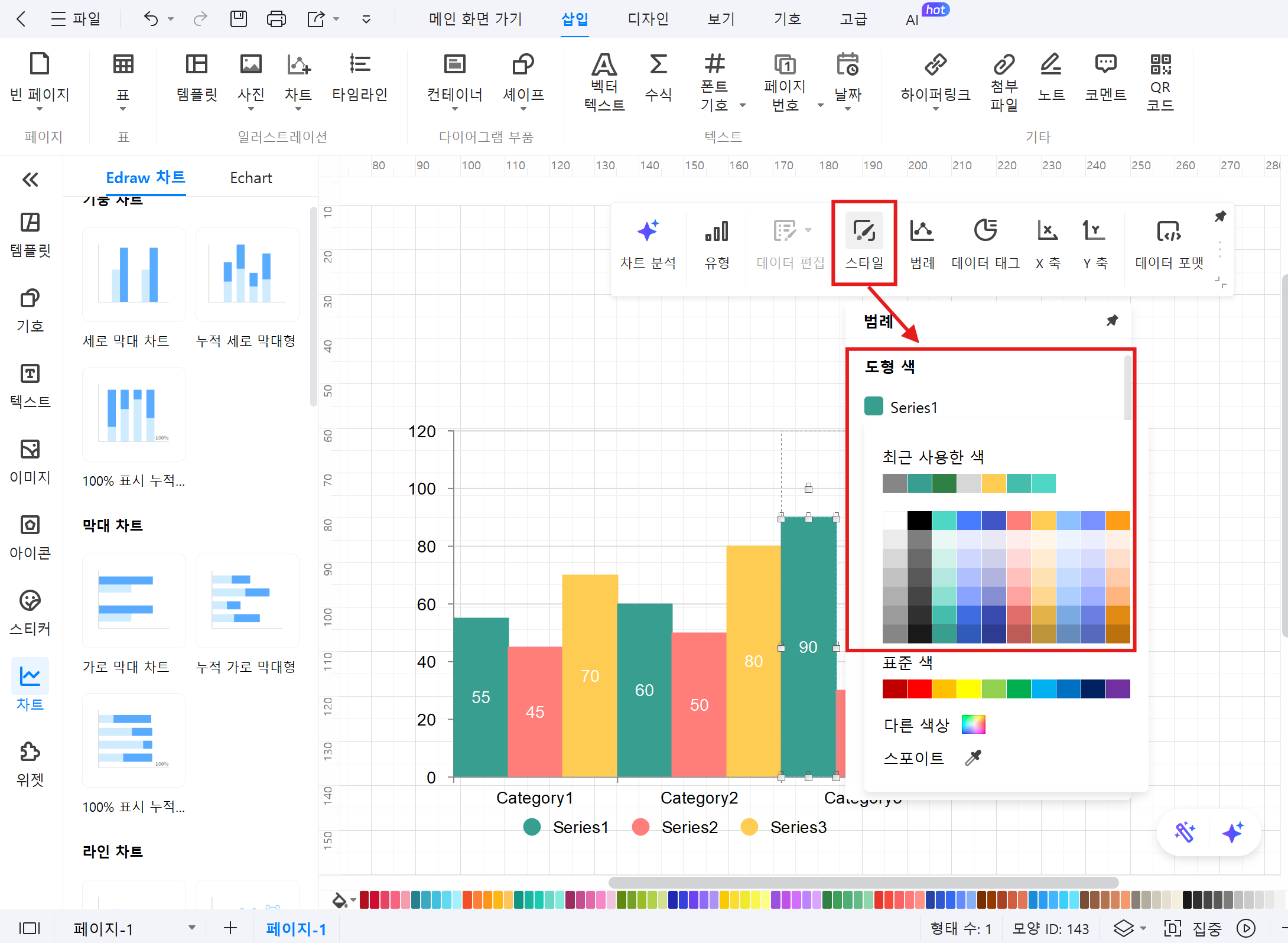
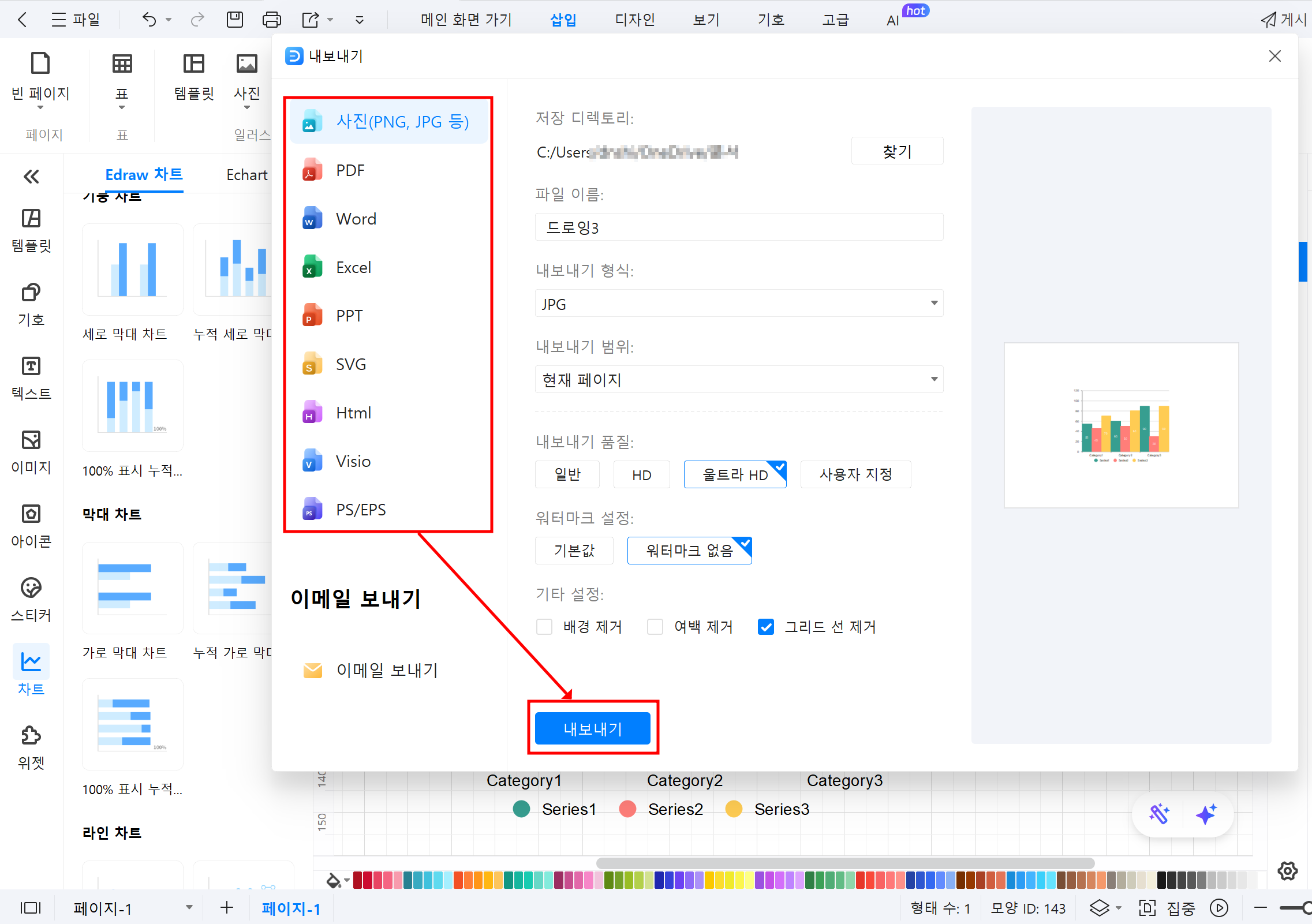
⑤ 저장 및 내보내기: 완성된 히스토그램을 저장하거나 이미지로 내보냅니다.
2) 막대그래프 만들기
① 이드로우맥스(EdrawMax) 실행: EdrawMax를 실행하고 ‘새로 그리기’를 엽니다.
② 차트 템플릿 선택: ‘차트’ 카테고리에서 막대그래프 템플릿을 선택합니다.
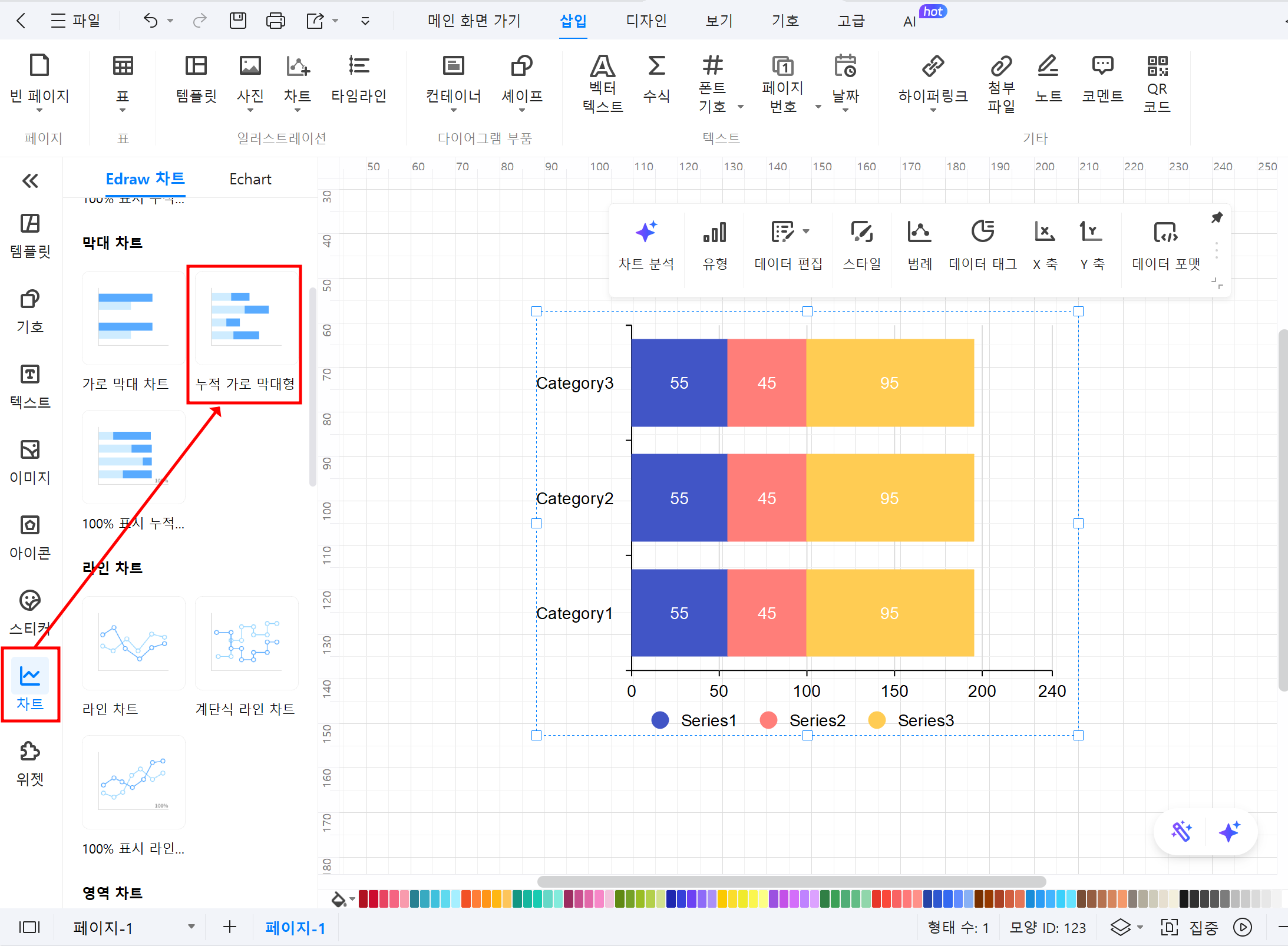
③ 데이터 입력: ‘데이터 편집’을 클릭하여 원하는 데이터로 변경합니다.
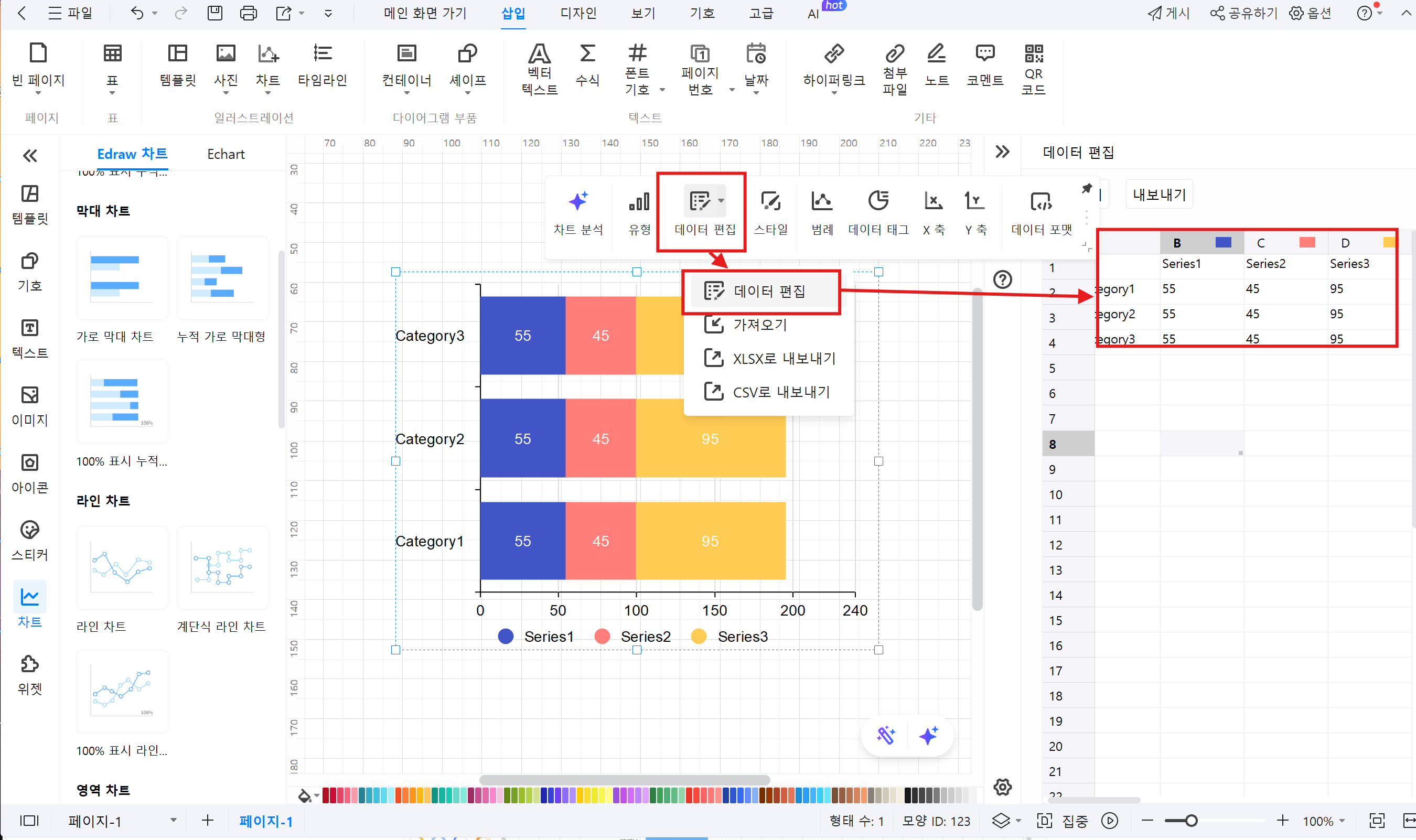
④ 막대 색상 및 간격 조정: 막대그래프는 막대 간 간격이 중요하므로 필요에 따라 간격을 조정하고, 색상으로 각 항목을 구분할 수 있습니다.
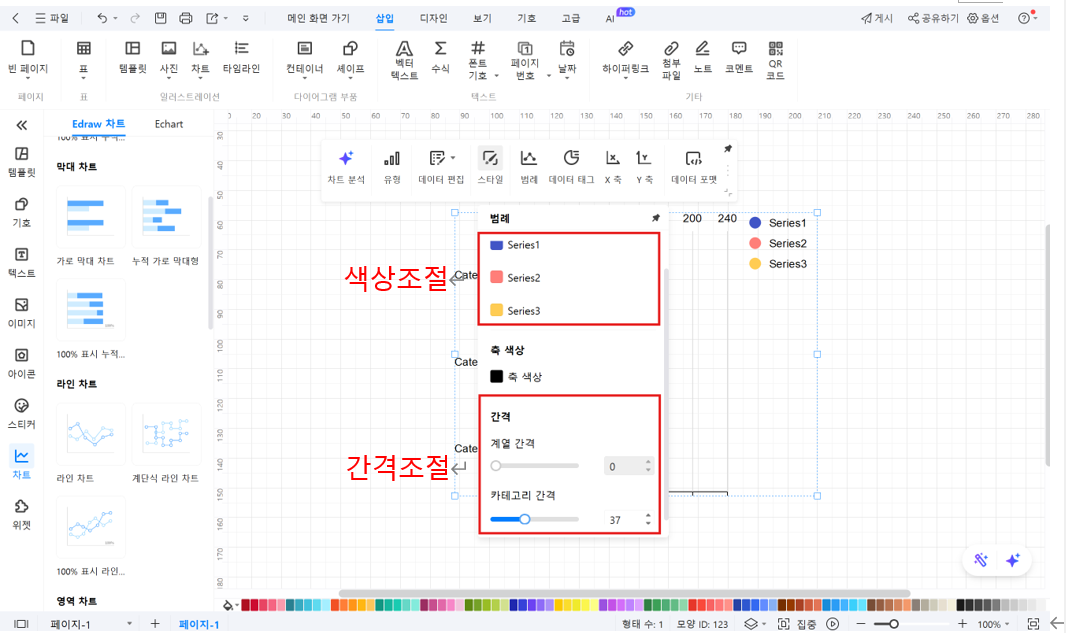
⑤ 저장 및 내보내기: 완성된 막대그래프를 저장하거나 다양한 형식의 파일로 내보내기 및 공유가 가능합니다.
마치며
EdrawMax(이드로우맥스)는 직관적인 인터페이스를 통해 히스토그램과 막대그래프를 쉽고 빠르게 제작할 수 있는 프로그램입니다. 사용자는 데이터를 입력하고, 색상이나 레이블 등을 간단히 수정하여 보기 좋은 그래프를 만들 수 있습니다. 시각적으로 깔끔한 히스토그램과 막대그래프를 통해 한층 더 편리해진 데이터 분석을 경험해 보세요.

