Diagrama de Euler - Definição, Modelos, Ferramenta
O Que é um Diagrama de Euler
Um diagrama de Euler é uma ferramenta gráfica que representa as relações dos sujeitos representados no gráfico. Os diagramas Euler são frequentemente utilizados nos campos da educação e dos negócios.
Comparado com o diagrama de Venn, o diagrama de Euler só mostra conexões relevantes entre os tópicos. Por exemplo, todos os seres vivos com quatro patas são animais, mas, nem todos os animais têm quatro patas, como os peixes. Eles só têm uma cauda, mas pertencem à família dos animais. Deste ponto de vista, é evidente a relação entre os animais e as quatro patas. Em matemática, chamamos isso de relação de inclusão.
As quatro patas são um subconjunto de animais. Entretanto, um mineral não está relacionado com os animais porque não há semelhanças; um outro círculo azul representa o mineral. E não há nenhuma parte sobreposta entre o círculo de animal e mineral.
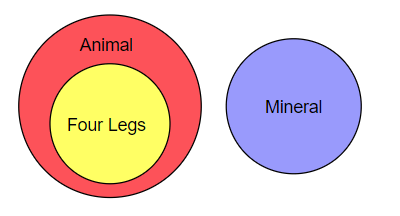
Fonte da imagem: en.wikipedia.org
Outro exemplo dum diagrama de Euler são as relações entre diferentes objetos do Sistema Solar.
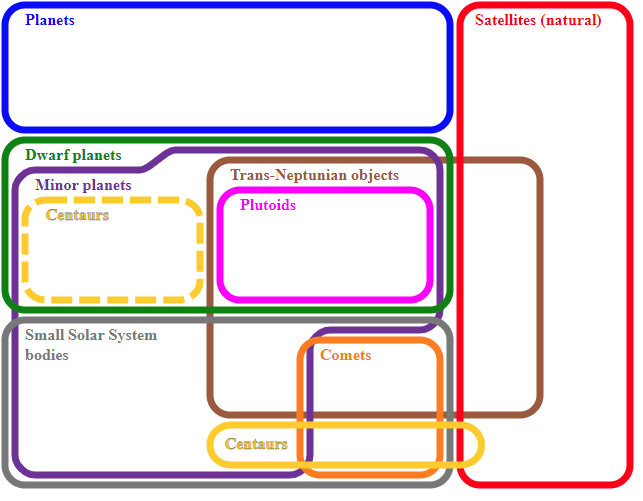
Fonte da imagem: en.wikipedia.org
Primeiro, o plano é separado pelas curvas do diagrama de Euler em duas partes; a zona interior representa os elementos dos conjuntos, enquanto a exterior mostra todos os elementos excluindo os conjuntos do planeta. Além disso, as curvas de sobreposição significam apenas a relação de inclusão. Se nenhuma curva se estiver cruzando ou intercruzando, os elementos não são membros dos conjuntos.
Os elementos comuns aos dois conjuntos estão somente na zona sobreposta dentro de ambas as curvas, e o subconjunto dum conjunto é circundado pelas curvas dentro do interior doutro conjunto. A partir desta imagem, fica claro como o diagrama de Euler é diferente e como esclarece os assuntos complexos.
Portanto, os diagramas de Euler consistem em algumas formas ou círculos claros, demonstrando as relações positivas entre esses conjuntos.
Diagramas de Venn vs. Diagramas de Euler
A maior parte das pessoas confundem os diagramas Venn com os diagramas Euler. Os "Círculos Eulerianos", cunhados pelo matemático suíço Leonhard Euler (1707–1783), são incorporados juntamente com os diagramas Venn como ferramentas de instrução da teoria do conjunto.
Os diagramas Venn, a forma mais criativa dos diagramas Euler, consistem em todas as segundas zonas logicamente possíveis de sobreposição entre as suas curvas n e concentram-se em todas as relações de inclusão/exclusão dos seus conjuntos. O preto indica as regiões de exclusão, o que significa que as regiões que excluem o conjunto seriam pretas.
Mas, os diagramas de Euler só devem ser coloridos na sobreposição, o que significa que somente as regiões incluindo o conjunto seriam coloridas. Portanto, a diferença mais significativa é a sobreposição das partes relacionadas. Normalmente, as relações poderiam se dividir em duas partes: relevância e irrelevância. Um diagrama de Venn mostraria tanto relevância quanto irrelevância entre os sujeitos, mas tanto relevância quanto irrelevância existem nos diagramas de Euler.
Tomando os mamíferos e as aves como exemplo, as aves não podem ser classificadas como mamíferos porque as aves são espécies que põem ovos ao contrário dos vivíparos, portanto, as aves são irrelevantes para os mamíferos. No diagrama Venn, os círculos dos mamíferos e das aves devem ser sobrepostos de forma representativa, enquanto os seus círculos no diagrama de Euler não devem ser cruzados. Portanto, os diagramas Venn e Euler mostram a irrelevância dos sujeitos duma maneira totalmente distinta.
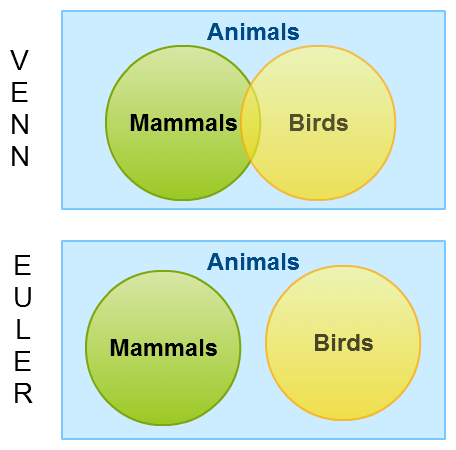
Fonte da imagem: creately.com
Modelos de Diagrama de Euler
1. Este modelo mostra a relação entre países nas Ilhas Britânicas.
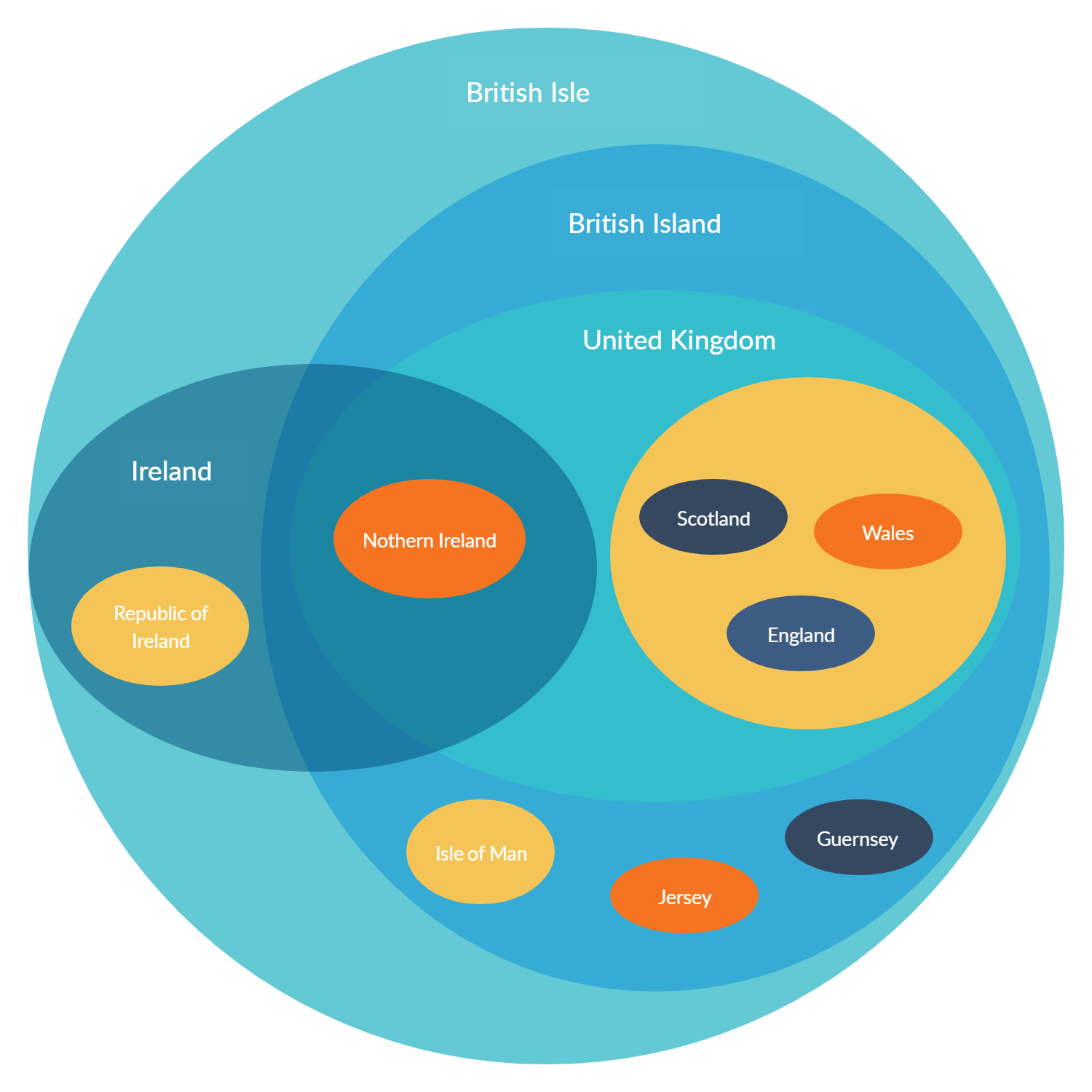
Fonte da imagem: pinterest.ca
2: O modelo mostra a relação das cores do baralho.
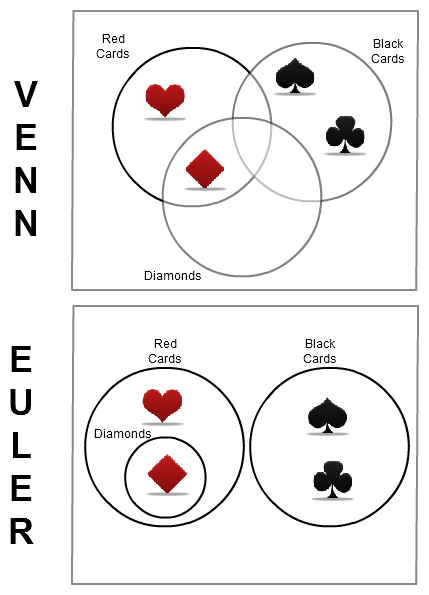
Fonte da imagem: /creately.com/
3: Este modelo demonstra as relações entre magia, feiticeiros e lagartos. A magia inclui feiticeiros, mas é irrelevante para os lagartos.
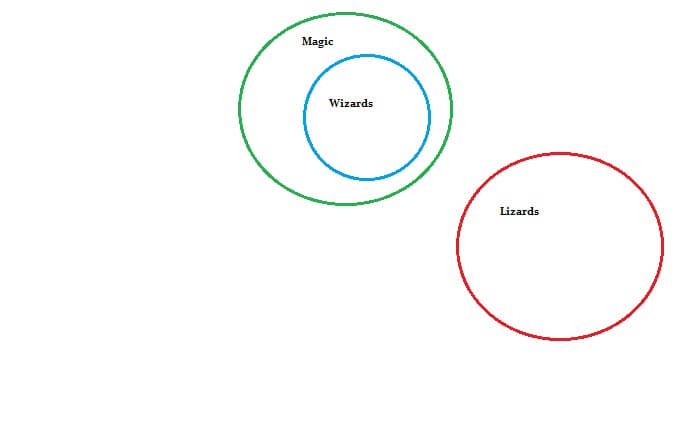
Fonte da imagem: statisticshowto.com
4: Este diagrama de Euler demonstra as relações geográficas da região da Oceania, que se divide em 4 sub-regiões: Melanésia, Micronésia, Polinésia e Australásia.
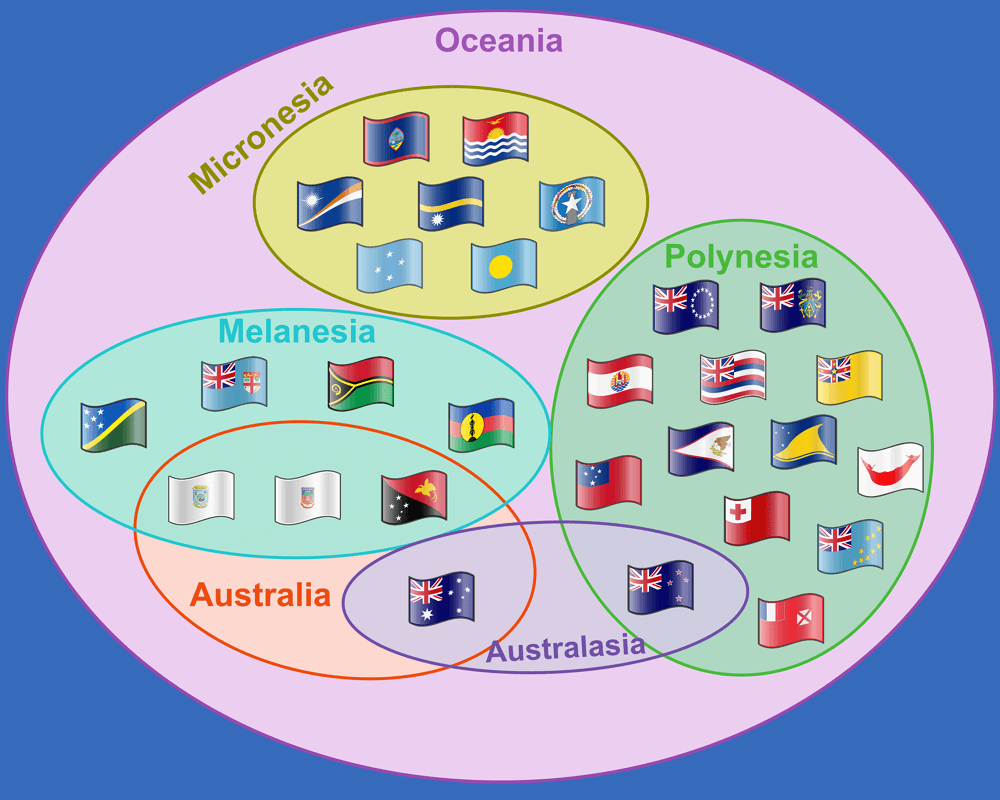
Fonte da imagem: reddit.com
EdrawMax
Software de Diagrama Tudo-em-um
- Compatibilidade de arquivo superior: Importe e exporte desenhos para vários formatos de arquivo, como o Visio
- Compatível com várias plataformas (Windows, Mac, Linux, Web)
Como Você Pode Fazer um Diagrama de Euler
Você pode usar qualquer ferramenta gráfica e software, mas se você tiver de fazer diagramas de Euler complexos, o EdrawMax pode ser uma boa escolha.
Passo 1: Pense no objetivo como vai utilizar os seus diagramas de Euler.
- Quantos quadrados ou círculos você precisa?
- Com quais relações os seus tópicos irão interagir?
Passo 2: Encontre o formato e interseções que você deseja inserir.
Passo 3: Rapidamente salve e baixe a visão que você quer.
Se você vai criar diagramas Euler complexos, é uma ferramenta de diagramação abrangente com designs personalizados e imensos modelos à sua disposição.
Dicas para Você Fazer um Diagrama de Euler
Há algumas restrições ao fazer diagramas de Euler:
1: O primeiro é um diagrama Venn com 4 contornos, não o diagrama normal de Euler, mas os dois seguidos são diagramas de Euler. A diferença está no seu aspeto e estética. O segundo com círculos poderia tornar os diagramas mais compreensíveis e comparar os elementos de cada conjunto. Ademais, a mudança é mais eficaz para que as pessoas entendam as informações que os diagramadores apresentam.
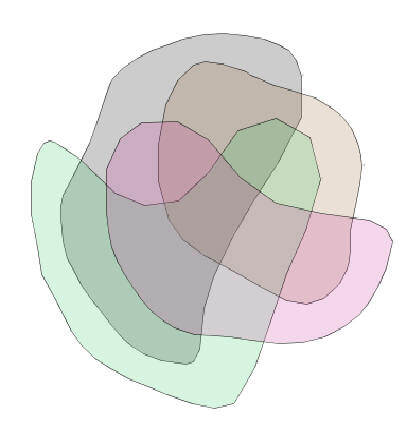
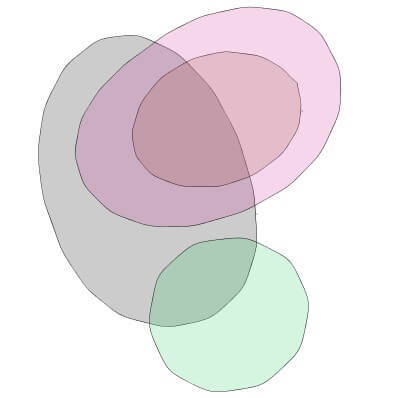
Fonte da imagem: cs.kent.ac.uk
O primeiro é um diagrama Venn com 4 contornos, não o diagrama padrão de Euler, mas os dois seguidos são. A diferença está relacionada com a aparência estética.
O segundo com círculos poderia tornar os diagramas mais compreensíveis e comparar os elementos de cada conjunto. Além disso, a mudança é mais eficaz para que as pessoas entendam as informações que os diagramadores apresentam.
2: Há apenas dois contornos que se cruzam no máximo, devido à impraticabilidade dos pontos triplos. Na imagem que você observou, não é permitido desenhar isto. Se você fizer isso, será com os diagramas de Venn, não com os diagramas de Euler. Por favor, dedique mais tempo aos exemplos e modelos dos diagramas de Euler.
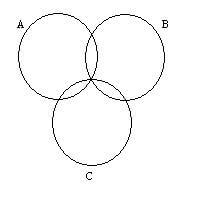
Fonte da imagem: cs.kent.ac.uk
Este diagrama também não é o diagrama padrão de Euler porque as zonas A, B, C são representadas e entrecruzadas por um ponto triplo. Isto quebra as regras 2 e 4.
3: Como a borda dos contornos não pode ser demonstrada por segmentos de linha, ela não pode ter Contornos simultâneos.
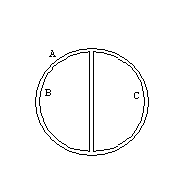
Fonte da imagem: cs.kent.ac.uk
Este diagrama mostra as zonas AB e AC, e duas zonas pertencem a um conjunto. Entretanto, as zonas AB e AC não têm elementos comuns.
4: Nos diagramas Euler, as zonas sem conexão não devem aparecer duas vezes ou mais.
5: Não é permitido cruzar contornos nos diagramas de Euler se os contornos dos diagramas de Euler forem as curvas simples.
Conclusão
O segredo para dominar os diagramas e Euler é entender a diferença entre os diagramas de Venn e de Euler. O processo de elaboração não é lá muito difícil para as pessoas, portanto, antes de desenhar os diagramas de Euler, você poderia encontrar mais modelos e exemplos a usar e pensar em como você pode representar a sua ideia neste diagrama com base noutros diagramas de Euler. A prática leva à perfeição.